You may have heard some of the news stories about E8, such as:
- E8 provides the densest sphere packing in 8 dimensions (media, arxiv).
- Experimental physicists reported detecting “emergent E8 symmetry” in the laboratory, corroborating predictions made 20 years earlier by Zamolodchikov and others. The experiment is fascinating on its own, even ignoring the connection with E8. For an exposition of this aimed at mathematicians, see my paper with David Borthwick.
- The “calculation the size of Manhattan” was widely reported in the news media in 2007. This was the result of some serious mathematical effort by the Atlas of Lie groups project. They calculated the Kazhdan-Lusztig-Vogan polynomials for the split real E8. David Vogan described it for mathematicians in this paper.
- The “Exceptionally Simple Theory of Everything” claimed to unify the four fundamental forces of physics using a real form of E8. This turned out to be no more scientific than cold fusion; see my paper with Jacques Distler for a disproof. It was described in an article in Ars Technica.
E8 is also mentioned as playing a role in the fictional Beard-Einstein Conflation in the novel Solar by Ian McEwan.
But what does “E8” mean?
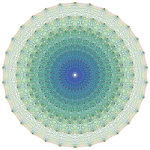
Picture of the E8 root system
It can be:
- a root system. This is a collection of 240 points in 8-dimensional space. The graphic you see here shows a projection of it into a well-chosen plane.
- a lattice in 8-dimensional space.
- a complex Lie group. The Wikipedia entry on E8 gives an introduction to this and the two items below.
- one of three different real Lie groups whose complexification is the complex Lie group E8.
- an algebraic group over a field related to the complex Lie group
New developments
There have been exciting recent developments about E8 also in pure mathematics, especially related to cohomological invariants.
- Nikita Semenov constructed a degree 5, modulo 2 cohomological invariant. This settled a long-standing question of Serre’s. It was further applied to studying embeddings of finite simple groups in the complex E8.
- The Rost invariant (degree 3) modulo 5 has an explicit formula determined by Philippe Gille and Anne Quéguiner-Mathieu.
- The kernel of the Rost invariant (degree 3) modulo 3 is known by Vladimir Chernousov, and this has been reproved using Chow motives by myself, Victor Petrov, and Nikita Semenov.
- Serre’s Conjecture II was proved for function fields of complex surfaces by de Jong, He, and Starr.
- The torsion index of E8 was calculated to be 2880 by Burt Totaro in two papers.
- The Kneser-Tits Conjecture was just settled for one of the two rank-2 forms of E8 by Parimala, Jean-Pierre Tignol, and Richard Weiss.
- Bob Guralnick and I showed that E8 can be viewed as the stabilizer of a degree 8 homogeneous polynomial on a 248-dimensional vector space, or the automorphism group of a commutative nonassociative 3875-dimensional algebra. Later, Maurice Chayet and I explicitly described the multiplication on this algebra and it was described as a decomposition algebra by De Medts and Van Couwenberghe.
A survey article
For a more detailed and technical discussion of these subjects, see the survey in Bulletin of the AMS.
Here are some things that should have appeared in the survey article but didn’t:
- A question: For the fundamental Weyl modules of E8, it is known for which characteristics they are irreducible. In the cases where they are reducible, the composition factors do not seem to be known, even down to specific questions such as whether the trivial module occurs in the head of the radical.
- A reference: The end of the paper “Finite H-spaces and Lie groups” by J.F. Adams contains a “Letter from E8“. Recommended reading!