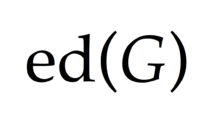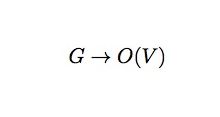Over the past year, several people have written to me for clarification about the stabilizer in Spin14 of a generic vector in one of its half-spin representations. My 2017 paper Spinors and essential dimension with Robert Guralnick shows that, over an algebraically closed field of characteristic different from 2, the stabilizer is \(G_2 \times G_2\)…
Back in the 1970s and 1980s, a bunch of people proved a host of results about finite-dimensional irreducible representations of simple Lie algebras over the complex numbers. They discovered a startling dichotomy: in various ways, small representations behave similarly to each other and large representations behave similarly to each other. Moreover, the difference between “small”…
If you love semisimple Lie algebras, like I do, then you should take a look at Meinolf Geck’s paper On the construction of semisimple Lie algebras and Chevalley groups that just appeared in Proceedings of the AMS (journal version, preprint version). He gives an elementary and canonical construction of a semisimple complex Lie algebra from its…
My survey E8, the most exceptional group will appear in an upcoming issue of Bulletin of the American Mathematical Society. It talks about the history and recent results on E8, focusing on the algebraic perspective of Lie algebras, Lie groups, and algebraic groups. You can read the article here or get an inkling of some the…
Updated June 10, 2016 I have two new papers out, both joint with Bob Guralnick: Spinors and essential dimension: We show that certain representations of the spin group Spinn are generically free for n > 14 and calculate the generic stabilizer for n ≤ 14, for all base fields. This shows that the formula for the…
New preprint out now: Tits p-indexes of algebraic groups, joint with Charles De Clercq. We give a `localized at a prime p‘ version of the results in Jacques Tits‘s classic 1966 paper Classification of semisimple algebraic groups. In that paper, he introduced the index of a semisimple group and classified all the possible values it…
My paper “Simple groups stabilizing polynomials“, written with Bob Guralnick, has appeared in Forum of Mathematics Pi. In it, we show that, if a simple algebraic group G stabilizes a polynomial function f on a vector space V, then with a very short list of exceptions G is actually the identity component of the stabilizer of f. We give various concrete applications of…
New preprint out today: Outer automorphisms of algebraic groups and a Skolem-Noether theorem for Albert algebras, written with Holger P. Petersson. In it, we study the question of existence of outer automorphisms of simple algebraic groups. One knows that the *-action and the Tits class provide obstructions to the existence of outer automorphisms, and the question is…
In my new preprint Bilinear and quadratic forms on rational modules of split reductive groups, written with Daniel K. Nakano, we extend the beautiful and classical theory of orthogonal and symplectic representations of split reductive groups in characteristic zero to prime characteristic. The two main new technical challenges are that orthogonal representations in characteristic 2 are connected with quadratic…
My paper Shells of twisted flag varieties and the Rost invariant, joint with Victor Petrov and Nikita Semenov, will appear in Duke Mathematical Journal. We introduce new techniques for studying the Krull-Schmidt decomposition of mod p Chow motives of projective homogeneous varieties, by generalizing Vishik’s notion of shells on quadrics to arbitrary projective homogeneous varieties. We then apply our techniques…