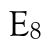If you love semisimple Lie algebras, like I do, then you should take a look at Meinolf Geck’s paper On the construction of semisimple Lie algebras and Chevalley groups that just appeared in Proceedings of the AMS (journal version, preprint version).  He gives an elementary and canonical construction of a semisimple complex Lie algebra from its root system.  It is a pleasing read.

He explains that it is a retelling of results on quantum groups from various works by George Lusztig, made simpler by translating them into the context of semisimple Lie algebras.

The construction goes by defining a vector space M with basis corresponding to a Chevalley basis of the Lie algebra —  in this language a copy of the root system and a copy of the set of simple roots — and specific elements of gl(M), namely one element for each of the root subalgebras corresponding to plus or minus a simple root.  He shows that the Lie subalgebra of gl(M) generated by these elements is semisimple with root system the one you started with.