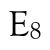Over the past year, several people have written to me for clarification about the stabilizer in Spin₁₄ of a generic vector in one of its half-spin representations. My 2017 paper Spinors and essential dimension with Robert Guralnick shows that, over an algebraically closed field of characteristic different from 2, the stabilizer is \(G_2 \times G_2\) (and in particular the stabilizer is connected). People ask about this because there is an earlier paper that claims the generic stabilizer is not connected, that \(G_2 \times G_2\) has index 2 in the stabilizer. I’ll explain here a way to see that \(G_2 \times G_2\) is the right answer.

It is easier to see what is happening in SO₁₄. There one can see directly that the image of \(G_2 \times G_2\) has normalizer \((G_2 \times G_2) \rtimes \mu_4\), see p.62 of my 2009 Memoir of the AMS “Cohomological invariants” or in Markus Rost’s note “On 14-dimension quadratic forms, their spinors, and the difference of two octonion algebras“. In the \(\mu_4\) component of the normalizer of \(G_2 \times G_2\), you find that the element of order 2 is the linear transformation -1, which is in the center. (The inverse image of -1 in Spin₁₄ is a 4th root of unity generating the center, which acts on the half-spin representation as a 4th root of unity and so does not fix a generic vector.)

Therefore, the normalizer of \(G_2 \times G_2\) in Spin₁₄ is \((G_2 \times G_2) \rtimes \mu_8\), where a generator of the \(\mu_8\) interchanges the two \(G_2\)’s and is a square root of a generator of the central \(\mu_4\) in Spin₁₄.  (This element is written explicitly in my Memoir.)  For the earlier paper’s claim to be true, the element of order 2 in the \(\mu_8\) — a 4th power of a generator of the \(\mu_8\) — would have to interchange the two copies of \(G_2\).  But its image in SO₁₄ is 1, which doesn’t interchange the two components. Therefore, the stabilizer of a generic vector in the half-spin representation is \(G_2 \times G_2\) and no larger.

I am not sure what went wrong in the earlier paper.  Perhaps the author found an element that lies not in Spin but in some slightly larger group.  For example, if you consider \(G_2 \times G_2\) in SO₁₄, there is an element of O₁₄ of order 2 (namely, the matrix that interchanges the two components and multiplies by -1, see the first paragraph on p.547 of my 2017 paper on Spin groups) that normalizes \(G_2 \times G_2\).